티스토리 뷰
머신러닝 모델에서 훈련 데이터가 매일 추가되는 경우를 생각해보자.
훈련 데이터가 한번에 준비되는 것이 아니라, 조금씩 전달된다고 가정하면, 어떤 알고리즘으로 모델을 만들어야 할 지 애매하다. 데이터가 쌓일 때까지 무작정 기다렸다가 훈련을 시키는 것도 이상하고, 기존 훈련 데이터에 새로운 데이터를 항상 추가한 모델을 매일 다시 훈련한다면 나중에는 훈련 데이터가 감당할 수 없을만큼 많아질 것이다.
그렇다고 기존 훈련 데이터를 버리자니, 버린 데이터가 특정 타깃의 마지막 데이터였다면 더 이상 그 타깃은 제대로 예측할 수 없을 것이다.
가장 좋은 방법은 훈련한 모델을 버리지 않고 새로운 데이터에 대하여만 조금씩 더 훈련을 하는 것이다.
이렇게 하면 훈련한 모델을 버리지 않고, 사용한 데이터를 모두 유지할 수 있다.
이런 식의 훈련 방식을 점진적 학습 또는 온라인 학습이라고 부른다.
대표적인 점진적 학습 알고리즘이 바로 이번 포스팅에서 다룰 확률적 경사 하강법이다.
바로 한번 알아보자.
확률적 경사 하강법
확률적 경사 하강법은 말 그대로 경사를 따라서 내려가는 방법이다.
산을 생각하고 비유하면 편하다.
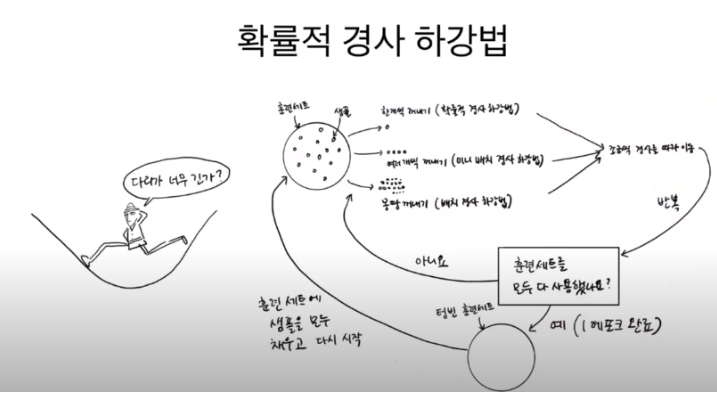
훈련 세트에서 랜덤하게 하나의 샘플을 선택하여 가파른 경사를 조금 내려간다. 그 다음 훈련 세트에서 랜덤하게 또 다른 샘플을 하나 선택하여 경사를 조금 더 내려간다. 이런 식으로 전체 샘플을 모두 사용할 때까지 계속 반복하여 훈련을 하는 방식이라고 생각하면 편하다.
모든 샘플을 다 사용했는데도 불구하고 산을 모두 다 내려오지 못했다면, 다시 처음부터 반복하면 된다.
확률적 경사 하강법에서 하나의 훈련 세트를 모두 사용하는 과정을 에포크라고 부르며, 일반적으로 경사 하강법은 수십, 수백번 이상의 에포크를 수행한다.
경사 하강법은 한번에 꺼내는 샘플 횟수에 따라 그 종류가 정해진다.
한번에 모든 훈련 세트를 전부 꺼내 훈련하는 것이 배치 경사 하강법, 한번에 여러 개씩 꺼내는 방식이 미니 배치 경사법, 1개씩 꺼내는 방식이 확률적 경사 하강법이다.
확률적 경사 하강법을 사용하면 훈련 데이터가 모두 준비되어 있지 않고, 매일매일 업데이트되어도 학습을 계속 이어나갈 수 있다.
그런데 확률적 경사 하강법은 도대체 어디서 내려가는 걸까? 확률적 경사 하강법이 내려가려고 하는 산은 바로 "손실 함수"라고 부르는 것이다.
손실 함수
손실 함수는 어떤 문제에서 머신러닝 알고리즘이 얼마나 엉터리인지를 측정하는 기준이다. 손실 함수의 값이 작을수록 모델이 적확한 것이지만, 어떤 값이 최솟값인지는 알 수 없다.
그렇기 때문에 확률적 경사 하강법을 사용하여 가능한 많이 찾아보고 만족할만한 수준이라면 산을 다 내려왔다고 인정하는 것이다.
손실 함수는 선형회귀에서 다뤘던 비용 함수의 또 다른 말이다. 엄밀히 말하면 손실 함수는 샘플 하나에 대한 손실을 정의하고, 비용 함수는 훈련 세트에 있는 모든 샘플에 대한 손실 함수의 합을 말한다.
분류에서의 손실은 간단하다. 정답을 못맞히는 것.
만약 4개의 샘플이 있다면, 정답률이 될 수 있는 후보는 0, 1/4, 1/2, 3/4, 1 이렇게 5가지 뿐이다.
이런 형태의 함수로는 확률적 경사 하강법을 사용할 수가 없다.
즉, 손실 함수는 연속적이여야 한다!
그럼 연속적인 손실함수는 어떻게 만드는 것인가?
손실 함수에도 여러 종류가 있지만, 가장 일반적으로는
이진 모델에서는 로지스틱 손실함수,
다중 모델에서는 크로스 엔트로피 손실함수이다.
- 로지스틱 손실함수
로지스틱 손실함수는 기본적으로 다음과 같다.
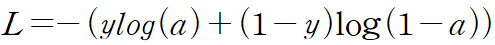
a는 활성화 함수가 출력한 값이고, y는 타깃 데이터이다.
즉, 이진 분류이기 때문에 양성 클래스인 1과 음성 클래스인 0의 2개의 정답만 있으므로, y가 1이거나 0인 경우로 정리된다.
- y가 1인 경우(양성 클래스) : -log(a)
- y가 0인 경우(음성 클래스) : -log(1-a)
위 두 식의 값을 최소로 만들다 보면 양성 클래스인 경우, a는 자연스럽게 1에 가까워지고, 반대로 음성 클래스인 경우에는 로지스틱 손실 함수의 값을 최소로 만들면 a가 0에 가까워진다.
다시 말해, 로지스틱 손실 함수를 최소화하면 a의 값이 우리가 가장 이상적으로 생각하는 값이 된다.
- 크로스 엔트로피 손실함수
사실 크로스 엔트로피 손실함수에서 y가 1과 0인 경우만 존재한다고 가정하고 푸는 것이 로지스틱 손실함수이다.
즉, 다중 모델의 경우에는 각 타깃 클래스가 나올 확률을 전부 적용하면 된다는 것이다.
크로스 엔트로피 손실함수는 여기에서 훨씬 자세하게 설명하고 있으니 참조하자.
이제 확률적 경사 하강법이 뭔지도 알았고, 손실함수의 개념에 대해서도 확인했으니 바로 코드와 함께 실습해보자.
직전 포스팅과 마찬가지로 데이터는 생선의 종류와 5가지 특성 데이터를 사용할 것이다.
데이터를 준비하고, 훈련 세트와 테스트 세트로 나눈 뒤, 스케일링까지 해주자.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
# 데이터 준비
fish = pd.read_csv('https://bit.ly/fish_csv_data')
print(fish.head())
# Species Weight Length Diagonal Height Width
# 0 Bream 242.0 25.4 30.0 11.5200 4.0200
# 1 Bream 290.0 26.3 31.2 12.4800 4.3056
# 2 Bream 340.0 26.5 31.1 12.3778 4.6961
# 3 Bream 363.0 29.0 33.5 12.7300 4.4555
# 4 Bream 430.0 29.0 34.0 12.4440 5.1340
print(pd.unique(fish['Species']))
#['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
# input 데이터
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
print(fish_input[:5])
# [[242. 25.4 30. 11.52 4.02 ]
# [290. 26.3 31.2 12.48 4.3056]
# [340. 26.5 31.1 12.3778 4.6961]
# [363. 29. 33.5 12.73 4.4555]
# [430. 29. 34. 12.444 5.134 ]]
# target 데이터
fish_target = fish['Species'].to_numpy()
# 훈련, 테스트 데이터 셋 나누기
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 데이터 전처리, 스케일 조정
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
이제 SGDClassifier 클래스를 호출하여 확률적 경사 하강법을 적용해보자.
loss 매개 변수를 log로 지정하면 로지스틱 손실함수를 적용하여 모델을 생성한다.
즉, 클래스마다 이진 분류 모델을 만든다. 예를 들어 도미의 경우는 도미를 양성 클래스로 두고 나머지를 음성 클래스로 두는 방식이다.
from sklearn.linear_model import SGDClassifier
# 확률적 경사 하강법을 사용하기 위한 함수
# loss = 손실 함수 지정, max_iter = 에포크 횟수
# loss = 'log' -> 로지스틱 손실함수
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.773109243697479
print(sc.score(test_scaled, test_target))
# 0.775훈련 세트와 테스트 세트 모두 정확도가 낮다. 아마 지정한 에포크 횟수가 부족해서 그런 거 같다.
확률적 경사 하강법은 점진적 학습이 가능한 모델이기 때문에 아래 코드와 같이 SGDClassifier 객체를 다시 만들지 않고, partial_fit() 메서드를 사용하여 호출할 때마다 1 에포크씩 이어서 훈련하도록 하자.
(SGDClassifier 는 기본적으로 샘플을 1개씩 뽑아서 사용하는 확률적 경사 하강법만 제공한다. 배치 경사 하강법이나 미니 배치 경사 하강법은 다음에 다루려고 한다.)
# 이번엔 partial_fit() 메서드를 사용하여 호출할 때마다 1 에포크 씩 이어서 훈련하도록 해보자.
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.8151260504201681
print(sc.score(test_scaled, test_target))
# 0.85정확도가 조금 올라가긴 했지만, 아직 만족할만한 수준은 아닌 거 같다.
그러나, 에포크를 무한정으로 돌릴 수 없는게 너무 많이 돌려버리면 훈련 세트에 과도하게 적합되는 과대적합 문제가 발생하여 테스트 세트의 정확도가 많이 떨어질 수 있다.
즉, 회귀 모델과 마찬가지로 적절한 에포크 횟수를 찾아야 한다는 것이다.
아래와 같이 300번 정도 에포크를 반복하며 점수를 저장해, 그래프로 나타내보자.
# 에포크가 너무 많은 횟수 진행되어 과대적합이 되기 전에 훈련을 바로 멈추는 것을 조기 종료라고 한다.
# 확률적 경사 하강 알고리즘은 에포크를 과소적합도, 과대적합도 아닌 적절한 시기에 끝내는 것을 목표로 한다.
import numpy as np
sc = SGDClassifier(loss='log', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()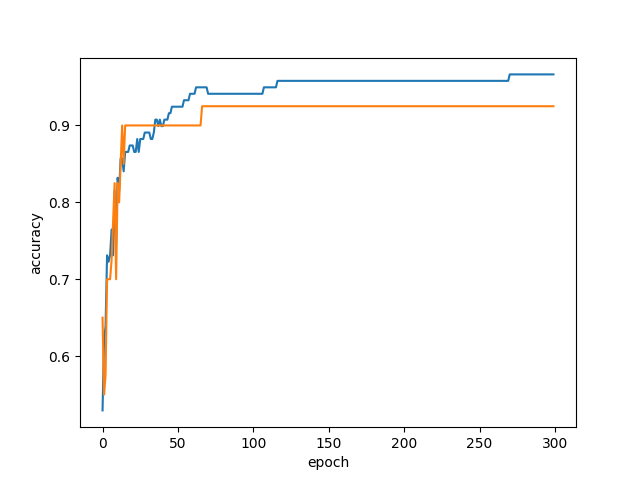
그래프를 보면, 에포크가 100 정도 일 때 훈련 세트와 테스트 세트의 정확도가 모두 높고, 그 차이도 많이 안난다.
적절한 에포크 횟수를 구했으니, 이제 에포크를 100에 맞추고 다시 모델을 훈련시키자.
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.957983193277311
print(sc.score(test_scaled, test_target))
# 0.925
print(sc.predict(test_scaled))
# ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch' 'Bream' 'Smelt' 'Roach' 'Perch'
# 'Pike' 'Bream' 'Perch' 'Bream' 'Parkki' 'Bream' 'Bream' 'Perch' 'Perch'
# 'Perch' 'Bream' 'Smelt' 'Bream' 'Bream' 'Bream' 'Bream' 'Perch' 'Perch'
# 'Roach' 'Smelt' 'Smelt' 'Pike' 'Perch' 'Perch' 'Pike' 'Bream' 'Perch'
# 'Roach' 'Roach' 'Parkki' 'Perch']
print(test_target)
# ['Perch' 'Smelt' 'Pike' 'Whitefish' 'Perch' 'Bream' 'Smelt' 'Roach'
# 'Perch' 'Pike' 'Bream' 'Whitefish' 'Bream' 'Parkki' 'Bream' 'Bream'
# 'Perch' 'Perch' 'Perch' 'Bream' 'Smelt' 'Bream' 'Bream' 'Bream' 'Bream'
# 'Perch' 'Perch' 'Whitefish' 'Smelt' 'Smelt' 'Pike' 'Perch' 'Perch' 'Pike'
# 'Bream' 'Perch' 'Roach' 'Roach' 'Parkki' 'Perch']기본적으로 SGDClassifier는 일정 에포크 동안 성능이 향상되지 않으면 더 훈련하지 않고 자동으로 멈춘다.
tol 매개변수에서 향상될 최솟값을 지정한다. 위 코드에서는 tol을 None으로 지정하여 자동으로 멈추지 않고 에포크를 반복시켰다.
결과를 확인해보면, 정확도도 꽤나 준수하고, 결과 또한 정확한 분류를 수행하고 있다.
전체 코드는 아래와 같으며, 경사 하강법은 머신 러닝에서 인공 신경망을 만들 때 꽤나 중요하게 쓰인다고 하니 반드시 확실하게 학습하고 가는 것이 좋아 보인다.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
# 데이터 준비
fish = pd.read_csv('https://bit.ly/fish_csv_data')
print(fish.head())
# Species Weight Length Diagonal Height Width
# 0 Bream 242.0 25.4 30.0 11.5200 4.0200
# 1 Bream 290.0 26.3 31.2 12.4800 4.3056
# 2 Bream 340.0 26.5 31.1 12.3778 4.6961
# 3 Bream 363.0 29.0 33.5 12.7300 4.4555
# 4 Bream 430.0 29.0 34.0 12.4440 5.1340
print(pd.unique(fish['Species']))
#['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
# input 데이터
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
print(fish_input[:5])
# [[242. 25.4 30. 11.52 4.02 ]
# [290. 26.3 31.2 12.48 4.3056]
# [340. 26.5 31.1 12.3778 4.6961]
# [363. 29. 33.5 12.73 4.4555]
# [430. 29. 34. 12.444 5.134 ]]
# target 데이터
fish_target = fish['Species'].to_numpy()
# 훈련, 테스트 데이터 셋 나누기
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 데이터 전처리, 스케일 조정
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
from sklearn.linear_model import SGDClassifier
# 확률적 경사 하강법을 사용하기 위한 함수
# loss = 손실 함수 지정, max_iter = 에포크 횟수
# loss = 'log' -> 로지스틱 손실함수
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.773109243697479
print(sc.score(test_scaled, test_target))
# 0.775
# 점수가 너무 낮다. 에포크 횟수가 부족해서 그런 거 같다.
# 이번엔 partial_fit() 메서드를 사용하여 호출할 때마다 1 에포크 씩 이어서 훈련하도록 해보자.
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.8151260504201681
print(sc.score(test_scaled, test_target))
# 0.85
# 에포크가 너무 많은 횟수 진행되어 과대적합이 되기 전에 훈련을 바로 멈추는 것을 조기 종료라고 한다.
# 확률적 경사 하강 알고리즘은 에포크를 과소적합도, 과대적합도 아닌 적절한 시기에 끝내는 것을 목표로 한다.
import numpy as np
sc = SGDClassifier(loss='log', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.957983193277311
print(sc.score(test_scaled, test_target))
# 0.925
print(sc.predict(test_scaled))
# ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch' 'Bream' 'Smelt' 'Roach' 'Perch'
# 'Pike' 'Bream' 'Perch' 'Bream' 'Parkki' 'Bream' 'Bream' 'Perch' 'Perch'
# 'Perch' 'Bream' 'Smelt' 'Bream' 'Bream' 'Bream' 'Bream' 'Perch' 'Perch'
# 'Roach' 'Smelt' 'Smelt' 'Pike' 'Perch' 'Perch' 'Pike' 'Bream' 'Perch'
# 'Roach' 'Roach' 'Parkki' 'Perch']
print(test_target)
# ['Perch' 'Smelt' 'Pike' 'Whitefish' 'Perch' 'Bream' 'Smelt' 'Roach'
# 'Perch' 'Pike' 'Bream' 'Whitefish' 'Bream' 'Parkki' 'Bream' 'Bream'
# 'Perch' 'Perch' 'Perch' 'Bream' 'Smelt' 'Bream' 'Bream' 'Bream' 'Bream'
# 'Perch' 'Perch' 'Whitefish' 'Smelt' 'Smelt' 'Pike' 'Perch' 'Perch' 'Pike'
# 'Bream' 'Perch' 'Roach' 'Roach' 'Parkki' 'Perch']
끝!!
'[Python] > Machine learning' 카테고리의 다른 글
| [ML] 지도 학습 7: 교차 검증과 그리스 서치 (0) | 2023.02.26 |
|---|---|
| [ML] 지도 학습 6: 결정 트리 (0) | 2023.02.26 |
| [ML] 지도 학습 4: 로지스틱 회귀 (0) | 2023.02.23 |
| [ML] 지도 학습 3: 다중 회귀(특성 공학과 규제) (0) | 2023.02.21 |
| [ML] 지도 학습 2: 선형 회귀 (0) | 2023.02.20 |
- react
- javascript
- 맛집
- AsyncStorage
- 정보보안기사 #실기 #정리
- Promise
- 이탈리안 레스토랑
- redux
- Async
- redux-thunk
- react-native
- await
- 인천 구월동 이탈리안 맛집
- 인천 구월동 맛집
- 파니노구스토
- Total
- Today
- Yesterday




