티스토리 뷰
합성곱 신경망(Convolutional Neural Network, CNN)은 필터링 기법을 인공 신경망에 적용함으로써 이미지를 더욱 효과적으로 처리하기 위해 고안되었다.
지난번 포스팅까지 다뤘던 인공 신경망에서는 각 뉴런마다 입력 개수만큼의 가중치가 존재했다. 즉, 모든 입력에 가중치를 곱하고 절편을 더하여 1개의 출력을 만드는 방식이었다.
예를 들어, 밀집층에 뉴런이 3개가 있다면 출력 또한 3개가 되며, 이는 입력 개수에 상관 없이 동일하다.
합성곱은 이러한 밀집층의 계산과는 조금 다르다. 입력 데이터 전체에 가중치를 적용하는 것이 아니라, 일부에 가중치를 곱한다.
즉, 가중치를 줄이는 효과가 있는데 특성이 어마어마하게 많아 가중치의 개수도 셀 수 없이 많은 이미지에서 연산량을 줄이고 효과적으로 처리할 수 있게 해준다.
예시로 9개의 특성이 존재한다고 했을 때, 아래 그림과 같이 4개의 특성에만 뉴런이 가지는 4개의 가중치(w0 ~ w3)을 곱하여 1개의 출력을 만드는 식이다.

그럼 최종적으로 4개의 특성을 가지는 은닉층이 생성이 되는데, 합성곱 신경망에서는 이를 특성맵이라고 부른다.

또한 특성맵을 만들기 위해 사용하는 뉴런(가중치)들을 필터 혹은 커널이라고 부른다.
이러한 방식의 장점은 커널를 굳이 1차원으로 만들지 않고 2차원 입력에도 충분히 적용할 수 있다는 점이다.
아래 그림과 같이 말이다.

밀집층에서 여러 개의 뉴런을 사용하듯이 합성곱 층에서도 여러 개의 필터를 사용할 수 있다. 아래 그림과 같이 여러 개의 필터를 사용하면 만들어진 특성 맵은 순서대로 차곡차곡 쌓이며, 만약 (2, 2) 크기의 특성 맵을 쌓으면 3차원 텐서가 되는 것이다.
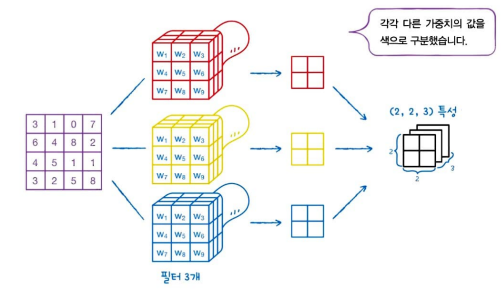
즉, 3개의 채널을 가진 텐서 데이터 또한 처리가 가능하다는 것이다.
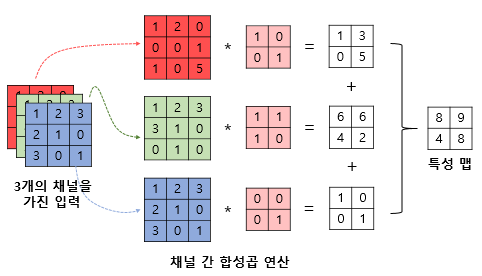
이렇게 원본 데이터의 차원 구조를 그대로 사용하기 때문에 합성곱 신경망이 이미지 처리 분야에서 뛰어난 성능을 발휘하는 것이다.
케라스 합성곱 층
Keras의 층은 모두 keras.layers 패키지 하위 클래스로 구현이 되어 있다.
합성곱 층은 아래와 같이 Conv2D 클래스를 사용한다.
from tensorflow import keras
keras.layers.conv2D(10, kernel_size=(3, 3), activation='relu')
kernel_size 매개변수로 필터에 사용할 커널의 크기를 지정하며, 출력에 사용할 활성화 함수도 지정해준다.
합성곱 신경망이란 즉, 1개 이상의 합성곱 층을 사용한 인공 신경망을 의미한다.
패딩과 스트라이드
1. 패딩
위에서 합성곱을 설명하며 (4, 4) 크기의 입력에 (3, 3) 크기의 커널을 적용하여 (2, 2) 크기를 가지는 특성맵을 만드는 그림이 있었다. 그런데 만약, 커널의 크기는 그대로 (3, 3)으로 두고 출력의 크기를 입력과 동일하게 (4, 4)로 만드려면 어떻게 해야 할까?
이 경우에는 더 큰 입력에 합성곱을 곱하는 시늉을 해야한다.
아래 그림을 확인해보자.

즉, (4, 4)의 입력을 (6, 6)인 입력인 것처럼 보이게 만든 뒤 특성맵을 만드는 것이다. 이렇게 입력 배열 주위를 가상의 원소로 채우는 것을 패딩이라고 한다.
실제 입력값이 아니기 때문에 패딩은 0으로 채우며, 패딩은 순전히 커널이 출력을 만드는 횟수를 늘려주는 것 밖에 없기 때문에 실제 계산에 어떤 영향을 끼치지는 않는다.
이렇게 입력과 특성 맵의 크기를 동일하게 만들기 위해 입력 주위에 0으로 패딩 하는 것을 세임 패딩(Same) 이라고 부른다.
합성곱 신경망에서는 이렇게 입력과 특성 맵의 크기를 동일하게 만드는 세임 패딩을 하는 경우가 아주 많다.
또한 패딩 없이 순수한 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 경우를 밸리드 패딩(Valid) 이라고 한다.
그럼 패딩은 왜 사용할까? (4, 4) 입력에서 패딩이 없다고 생각하면 아래와 같이 (3, 3) 커널이 특성 맵을 만들기 위해 찍는 횟수가 4번일 것이다.

가운데 4개의 특성은 커널이 4번 찍는 동안 4회에 걸쳐 특성맵을 만들지만, 모서리 부분은 각각 2번에서 꼭지점으로 가면 1회로 줄어든다. 이는 모서리 부분에 있는 중요한 정보가 특성 맵으로 잘 전달되지 않을 수도 있다는 것이다.
그렇기 때문에 패딩을 하여 모서리 부분까지 최소 4회는 특성 맵으로 전달이 되도록 하는 것이다.
즉, 적절한 패딩은 이미지의 주변에 있는 정보를 잃어버리지 않도록 도와준다.
keras.layers.conv2D(10, kernel_size=(3, 3), activation='relu', padding='same')
2. 스트라이드
위 예제에서는 합성곱 연산을 좌우, 위아래로 한 칸씩 이동했다. 하지만 두 칸씩 건너뛸 수도 있으며, 이렇게 두 칸씩 이동하면 당연히 만들어지는 특성 맵의 크기는 더 작아진다.
이런 이동의 크기를 스트라이드(stride)라고 한다.
기본적으로 스트라이드는 1이며, 아래와 같이 작성한다. 하지만 일반적으로 1보다 큰 스트라이드를 사용하는 경우는 드물기 때문에 스트라이드 매개변수를 입력하는 일은 잘 없다고 한다.
keras.layers.conv2D(10, kernel_size=(3, 3), activation='relu', padding='same', strides=1)풀링(Pooling)
폴링은 합성곱 층에서 만든 특성 맵의 가로세로 크기를 줄이는 역할을 수행한다.
예를 들어, 위 (4, 4) 입력의 특성 맵을 풀링해보면 아래와 같이 된다.
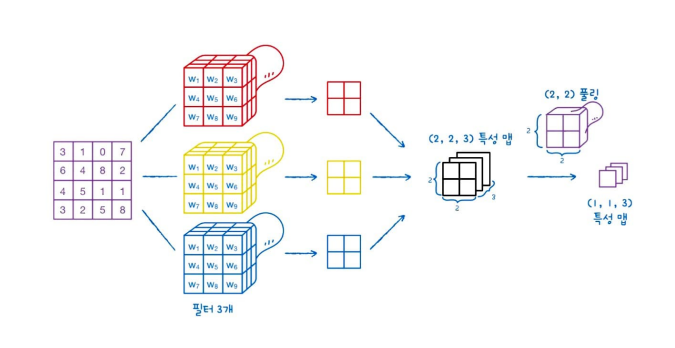
풀링은 커널을 찍는 영역에서 가장 큰 값을 고르는 최대 풀링과 평균 값을 계산하는 평균 풀링이 있는데, 최대 풀링을 예로 들면 아래와 같다.

풀링을 할 때는 각 영역이 겹치게 하면 안되기 때문에, 풀링의 크기 = 스트라이드 이다.
아래와 같이 풀링을 수행할 수 있다.
keras.layers.MaxPool2D(2)
평균 풀링의 경우는 다음과 같다.
keras.layers.AveragePooling2D(2)이번 글에서는 합성곱 신경망의 구조와 구성 요소들을 다뤄봤다.
전체적인 구조를 그림으로 나타내보자.
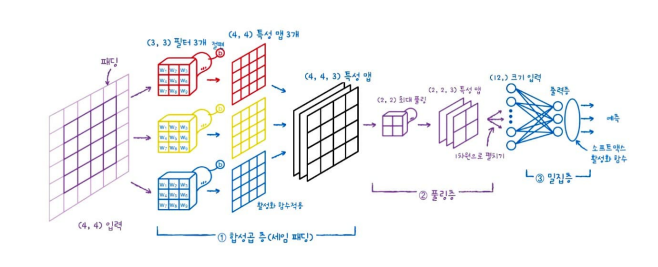
다음 포스팅에서는 이러한 합성곱 신경망을 이용하여 이미지를 분류하는 예제를 진행해보려고 한다.
끝!
'[Python] > Machine learning' 카테고리의 다른 글
| [ML] Deep Learning 5: CNN을 사용한 이미지 분류 (0) | 2023.03.07 |
|---|---|
| [ML] Deep Learning 3: 신경망 모델 훈련과 최상의 신경망 모델 얻기 (0) | 2023.03.06 |
| [ML] Deep Learning 2: 심층 신경망 (0) | 2023.03.06 |
| [ML] Deep Learning 1: 인공 신경망 (1) | 2023.03.05 |
| [ML] 비지도 학습 3: 주성분 분석 (0) | 2023.03.02 |
- Promise
- 인천 구월동 이탈리안 맛집
- react
- react-native
- 파니노구스토
- 이탈리안 레스토랑
- 맛집
- AsyncStorage
- await
- javascript
- 정보보안기사 #실기 #정리
- redux
- Async
- 인천 구월동 맛집
- redux-thunk
- Total
- Today
- Yesterday




